Time & Distance
Speed, Time and Distance:
Speed =
|
Distance
|
,
|
Time =
|
Distance
|
,
|
Distance = (Speed x Time).
| ||||
Time
|
Speed
|
- km/hr to m/sec conversion:
x km/hr =
|
x x
|
5
|
m/sec.
| ||
18
|
- m/sec to km/hr conversion:
x m/sec =
|
x x
|
18
|
km/hr.
| ||
5
|
- If the ratio of the speeds of A and B is a : b, then the ratio of the
the times taken by then to cover the same distance is
|
1
|
:
|
1
|
or b : a.
|
a
|
b
|
- Suppose a man covers a certain distance at x km/hr and an equal distance at y km/hr. Then,
The average speed during the whole journey is(2xy/x+y)km/hr.
Average and Relative Speed
If a body is moving with speeds s(1), s(2), s(3), ... s(n) and the time is constant for each part, then the average speed will be the Arithmetic Mean of the speeds.
If a body is moving with speeds s(1), s(2), s(3), ... s(n) and the distance is constantfor each part, then the average speed will be the Harmonic Mean of the speeds.
Relative Speed of two bodies moving towards each other s(1)+s(2) and in the same direction s(1)-s(2).
Boats, Streams and Escalators
If a constant distance is covered at speeds which are in an AP, then the times taken will be in an HP and vice-versa (For eg, Upstream, Boat-speed, Downstream speeds will always be in AP. Same can be applied in escalator questions as well).
Speed(Upstream) = S(Boat)-S(River)
Speed(Downstream) = S(Boat)+S(River)
Speed(Boat) = [S(Downstream)+S(Upstream)]/2
Speed(River) = [S(Downstream)-S(Upstream)]/2
Motion of two bodies in a straight line
Two bodies start from opposite ends P & Q at the same time and move towards each other with speeds S(1) & S(2). After meeting each other, they take times of T(1) & T(2) to reach their destinations.
Time taken for them to meet sqrt[T(1)*T(2)]
S(1)/S(2) = sqrt[T(2)/T(1)]
Two bodies start from opposite ends P & Q at the same time and move towards each other with speeds S(1) & S(2). They reach the opposite ends and reverse directions. {S(1)>S(2) and S(1)
Total distance covered till nth meeting (2n-1)D and time taken (2n-1)D/S(1)+S(2).
Circular Motion
Number of distinct points: In same direction, a-b and in opposite direction a+b (Here a/b is the reduced ratio of speeds).
PRACTICE QUESTIONS
Ex. Walking at 4 / 5 of its normal speed, a school bus is 10 minutes late. Find its usual time to cover the journey.
Solution : New Speed = 4 / 5 of original speed, since the speed and time has inverse relation so,
New Time taken by bus = 5 / 4 of the normal time
( 5 / 4 of usual time ) - ( usual time ) = 10 min.
1 / 4 of the normal time = 10 min
normal time = 40 min
Solution : New Speed = 4 / 5 of original speed, since the speed and time has inverse relation so,
New Time taken by bus = 5 / 4 of the normal time
( 5 / 4 of usual time ) - ( usual time ) = 10 min.
1 / 4 of the normal time = 10 min
normal time = 40 min
Ex. The distance between two stations Delhi and Lucknow is 500 km. A train starts at 5 pm from delhi and moves towards Lucknow at an average speed of 50 km / hr, Another train starts at 4.20 pm and moves towards delhi at an average speed of 70 km/hr. How far from delhi the two trains meet and at what time ?
Solution : Let the two trains meets at a distance of x km from delhi.
Now [Time taken by train from Lucknow to cover (500-x)km] - [Time taken by train from delhi to cover x km ] = 40 / 60

Solution : Let the two trains meets at a distance of x km from delhi.
Now [Time taken by train from Lucknow to cover (500-x)km] - [Time taken by train from delhi to cover x km ] = 40 / 60
Ex. Bullcart A cover a certain distance at the speed of 15 km/hr, another bullcart B covers the same distance at the speed of 16 km/hr. If Bull cart A takes 16 minutes longer than B to cover the same distance find the distance?
Solution : let the distance is x km
Time taken by A= x / 15 hrs
Time taken by B= x / 16 hrs

Solution : let the distance is x km
Time taken by A= x / 15 hrs
Time taken by B= x / 16 hrs
Ex. Ram can cover a certain distance in 1 hr 30 min. By covering two third of the distance at 4 kmph and the rest at 5 kmph. Find the total distance covered ?
Solution : Let the total distance be x km then:
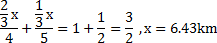
Solution : Let the total distance be x km then:
Ex. A train travells at average speed of 100 km / hr, it stops for 3 mins after travelling 75 kms of diatance. How long it takes to reach 600 kms from the starting point.
Solution : Time taken to travel 600 kms= 600 / 100 = 6 hrs
But it stop after travelling 75 kms , so number of stoping point in 600 kms will be= 600 / 75 = 8, but the last stoping point is actual end stoping so
Number of stoping point will be 7, and time taken= 7*3= 21 minutes
So total time = 6 hrs 21 mins
Solution : Time taken to travel 600 kms= 600 / 100 = 6 hrs
But it stop after travelling 75 kms , so number of stoping point in 600 kms will be= 600 / 75 = 8, but the last stoping point is actual end stoping so
Number of stoping point will be 7, and time taken= 7*3= 21 minutes
So total time = 6 hrs 21 mins
Ex. A is faster than B . A and B each walk 24 km. The sum of their speeds is 7 km / hr and the sum of their time taken is 14 hrs. Then A's speed is equal to :
Solution : Let A's speed = x km / hr and B's speed is = 7 - x km / hr

(x-3) (x-4) = 0
x=3, x=4, So A's speed is 4 km / hr, B's speed is 3 km / hr
Solution : Let A's speed = x km / hr and B's speed is = 7 - x km / hr
(x-3) (x-4) = 0
x=3, x=4, So A's speed is 4 km / hr, B's speed is 3 km / hr
Ex. A man on tour travels first 180 km at 60 km / hr and next 180 km at speed of 80 km / hr . The average speed of first 360 km of the tour is :
Solution : Total time taken = ( 180 / 60 ) + ( 180 / 80 ) = 21 / 4 hrs

Solution : Total time taken = ( 180 / 60 ) + ( 180 / 80 ) = 21 / 4 hrs
Ex. A train running at 3 / 7 of its own speed reached the destination in 14 hours, how much time could be saved if the train would have run at its own speed ?
Solution : New speed = 3 / 7 of normal speed
So, New Time will be = 7 / 3 of normal time. (Invers relation )
As 7 / 3 of normal time is = 14 hours
So, normal time = (14 * 3 / 7 ) = 12 hrs
So time saved = 14 - 12 = 2 hours
Solution : New speed = 3 / 7 of normal speed
So, New Time will be = 7 / 3 of normal time. (Invers relation )
As 7 / 3 of normal time is = 14 hours
So, normal time = (14 * 3 / 7 ) = 12 hrs
So time saved = 14 - 12 = 2 hours
Ex. Speed ratio of two school buses A and B in covering a certain distance is 4 : 5, If A takes 30 minutes more than B covering the distance, then time taken by B to reach the destination is :
Solution : Since speed ratio is 4 : 5
Time ratio will be 5 : 4 , let A takes 5x hrs and B takes 4x hrs to reach the destination then ,
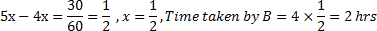
Solution : Since speed ratio is 4 : 5
Time ratio will be 5 : 4 , let A takes 5x hrs and B takes 4x hrs to reach the destination then ,
Ex. Steve traveled the first 2 hours of his journey at 40 mph and the last 3 hours of his journey at 80 mph. What is his average speed of travel for the entire journey?
Solution: Average speed of travel = 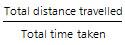
Total distance traveled by Steve = Distance covered in the first 2 hours + distance covered in the next 3 hours.
Distance covered in the first 2 hours = speed * time = 40 * 2 = 80 miles
Distance covered in the next 3 hours = speed * time = 80 * 3 = 240 miles
Therefore, total distance covered = 80 + 240 = 320 miles
Total time taken = 2 + 3 = 5 hours.
Hence, average speed =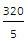 = 64 miles per hour.
= 64 miles per hour.
Total distance traveled by Steve = Distance covered in the first 2 hours + distance covered in the next 3 hours.
Distance covered in the first 2 hours = speed * time = 40 * 2 = 80 miles
Distance covered in the next 3 hours = speed * time = 80 * 3 = 240 miles
Therefore, total distance covered = 80 + 240 = 320 miles
Total time taken = 2 + 3 = 5 hours.
Hence, average speed =
Ex. Jane covered a distance of 340 miles between city A and city taking a total of 5 hours. If part of the distance was covered at 60 miles per hour speed and the balance at 80 miles per hour speed, how many hours did she travel at 60 miles per hour?
Solution: Let 'x' hours be the time for which Jane traveled at 60 miles per hour.
As the total time taken to cover 340 miles is 5 hours, Jane would have traveled (5 - x) hours at 80 miles per hour.
Distance covered at 60 miles per hour = Speed * time = 60 * x = 60x miles
Distance covered at 80 miles per hour = Speed * time = 80 (5 - x) = 400 - 80x miles
Total distance covered = Distance covered at 60 miles per hour + Distance covered at 80 miles per hour.
Therefore, total distance = 60x + 400 - 80x.
But, we know that the total distance = 340 miles.
Therefore, 340 = 60x + 400 - 80x
=> 20x = 60 or x = 3 hours.
As the total time taken to cover 340 miles is 5 hours, Jane would have traveled (5 - x) hours at 80 miles per hour.
Distance covered at 60 miles per hour = Speed * time = 60 * x = 60x miles
Distance covered at 80 miles per hour = Speed * time = 80 (5 - x) = 400 - 80x miles
Total distance covered = Distance covered at 60 miles per hour + Distance covered at 80 miles per hour.
Therefore, total distance = 60x + 400 - 80x.
But, we know that the total distance = 340 miles.
Therefore, 340 = 60x + 400 - 80x
=> 20x = 60 or x = 3 hours.
Ex. A runs 25% faster than B and is able to give him a start of 7 meters to end a race in dead heat. What is the length of the race?
Solution: A runs 25% as fast as B.
That is, if B runs 100m in a given time, then A will run 125m in the same time
In other words, if A runs 5m in a given time, then B will run 4m in the same time.
Therefore, if the length of a race is 5m, then A can give B a start of 1m so that they finish the race in a dead heat.
Start : length of race :: 1 : 5
In this question, we know that the start is 7m.
Hence, the length of the race will be 7 * 5 = 35m.
That is, if B runs 100m in a given time, then A will run 125m in the same time
In other words, if A runs 5m in a given time, then B will run 4m in the same time.
Therefore, if the length of a race is 5m, then A can give B a start of 1m so that they finish the race in a dead heat.
Start : length of race :: 1 : 5
In this question, we know that the start is 7m.
Hence, the length of the race will be 7 * 5 = 35m.
Ex. A bus travels from town A to town B. If the bus's speed is 50 km/hr, it will arrive in town B 42 min later than scheduled. If the bus increases its speed by 509 m/sec, it will arrive in town B 30 min earlier than scheduled. Find:
A) The distance between the two towns;
B) The bus's scheduled time of arrival in B;
C) The speed of the bus when it's on schedule.
A) The distance between the two towns;
B) The bus's scheduled time of arrival in B;
C) The speed of the bus when it's on schedule.
Solution: First we will determine the speed of the bus following its increase. The speed is increased by 509m/sec =50⋅60⋅6091000 km/hr =20 km/hr. Therefore, the new speed is V=50+20=70 km/hr. If x is the number of hours according to the schedule, then at the speed of 50 km/hr the bus travels from A to B within (x+4260) hr. When the speed of the bus is V=70 km/hr, the travel time is x−3060 hr. Then
50(x+4260)=70(x−3060)
5(x+710)=7(x−12)
72+72=7x−5x
2x=7
x=72 hr.
So, the bus is scheduled to make the trip in 3 hr 30 min.
The distance between the two towns is 70(72−12)=70⋅3=210 km and the scheduled speed is 21072=60 km/hr.
50(x+4260)=70(x−3060)
5(x+710)=7(x−12)
72+72=7x−5x
2x=7
x=72 hr.
So, the bus is scheduled to make the trip in 3 hr 30 min.
The distance between the two towns is 70(72−12)=70⋅3=210 km and the scheduled speed is 21072=60 km/hr.
Ex. Arun, Barun and Kiranmala start from the same place and travel in the same direction at speeds of 30, 40 and 60 km per hour respectively. Barun starts two hours after Arun. If Barun and Kiranmala overtake Arun at the same instant, how many hours after Arun did Kiranmala start?
Solution: As you can see that the speeds are in HP, so we can say that the times taken will be in AP. Time difference between Arun and Barun is 2 hours, so the time difference between Barun and Kiranbala will also be 2 hours.
Hence, Kiranbala started 4 hours after Arun
Ex. Two motorists Anil and Sunil are practicing with two different sports car; Ferrari and Maclarun, on the circular racing track, for the car racing tournament to be held next month. Both Anil and Sunil start from the same point on the circular track. Anil completes one round of the track in 1 min and Sunil takes 2 min to complete a round. While Anil maintains speed for all the rounds, Sunil halves his speed after the completion of each round. How many times Anil and Sunil will meet between 6th round and 9th round of Sunil (6th and 9th round is excluded)? Assume that the speed of Sunil remains steady throughout each round and changes only after the completion of that round.
Solution: Time taken by Sunil for 1st round = 2 min
2nd round = 4min
3rd round = 8 min
4th round = 16 min
5th round = 32 min
6th round = 64 min
7th round = 128 min
8th round = 256 min
⇒ Anil tales one minute for every round.
He meets 127 times in 7th and 255 times in 8th round
Total meet =127+255= 382
Ex. Mukesh, Suresh and Dinesh travel from Delhi to Mathura to attend Janmashtmi Utsav. They have a bike which can carry only two riders at a time as per traffic rules. Bike can be driven only by Mukesh. Mathura is 300km from Delhi. All of them walk at 15km/h. All of them start their journey from Delhi simultaneously and are required to reach Mathura at the same time. If the speed of bike is 60km/h, then what is the shortest possible time in which all three can reach Mathura at the same time?
Solution: Mukesh starts from Delhi (say A).
He has to take of the other two (say Dinesh) on his bike, take him up to a certain point(say C) drop him there and return for Suresh.
He has to take of the other two (say Dinesh) on his bike, take him up to a certain point(say C) drop him there and return for Suresh.
Meanwhile Suresh starts walking.
Suresh and Mukesh meet at (say B) Mukesh picks up Suresh at B and turn towards Mathura.
All of them arrive together at Mathura (say D).
Suresh and Mukesh meet at (say B) Mukesh picks up Suresh at B and turn towards Mathura.
All of them arrive together at Mathura (say D).
A------------ B ------------- C ------------- D
As, M drives at 60km/h and S (as well as D) walk at 15 km/h.
AC + CB = 4(AB)
BC+CB = 3(AB)
⇒ CB=1.5(AB)
Let AB=2, BC=3, (Also CD=2)
Actually, AB=600/7,BC=900/7,CD=600/7
Time taken=65/7hr
Ex. From a point P, on the surface of radius 3cm, two cockroaches A and B started moving along two different circular paths, each having the maximum possible radius, on the surface of the sphere, that lie in the two different planes which are inclined at an angle of 45 degree to each other. If A and B takes 18 sec and 6 sec respectively, to complete one revolution along their respective circular paths, then after how much time will they meet again, after they start from P?
Solution: Both the circular paths have the maximum possible radius hence, both have a radius of 3cm each. Irrespective of the angle between the planes of their circular paths, the two cockroaches will meet again , at the point Q only, which is diametrically opposite end of P.
A will takes 9 seconds to reach point Q, completing half a revolution. On the other hand, B would have completed 3/2 |
of his revolution and it will also reach point Q simultaneously.
No comments:
Post a Comment